Bitloops
I define a bitloop as a bit string (or bitstring) whose ends are connected to form a loop. The set of all bitstrings with n bits (the power set of n) can be partitioned by bitloops. The set of these bitloops can be partitioned by chains, which are sets of bitloops equipped with an operation defined below. The set of these chains can be partitioned by graphs. Every chain includes a cycle that generates a tessellation.
These elements are explained in detail below. See the original zine from 2020 (digital | print).
Let this Bitloop Calculator and Tesselator be a companion on your journey through the world of bitloops!
On the originality of this work: This is a blend of original ideas and mathematical fundamentals. I sourced the fundamentals from Wikipedia and Rotman's An Introduction to the Theory of Groups (1995), which I did not read past the second chapter. The original and sourced material are explained together for the sake of narrative. Original concepts are introduced in bold, often giving some existing word a local definition, and others are introduced in italics.
| Contents: |
| Bitloops |
| The Link |
| Patterns |
| Power Sets |
| Chains |
| Symmetry |
| Graphs |
| Tessellations |
| Catalogue |
| Appendix |
Bitloops
A bit is a number that is a zero or one. A bitstring is a sequence of bits. The bits in a bitstring are enclosed by square brackets. The letter n refers to the number of bits in the sequence, which is always a positive integer.
Examples are indicated by indentation.
[00001011] and [01010101] are bitstrings, each with n = 8 bits.
The elements in a bitstring are ordered and can be assigned indices. Let J be a set of n indices: {i1, i2, ... in}. The bits in a bitstring are assigned indices in order from left to right: [ i1 i2 ... in ].
Given the bitstring [01], i1 = 0 and i2 = 1.
A bitloop has n ordered bits, but the bits cannot be counted from 1 to n, because no bit comes first. For comparison, the seasons of the year have an order, but no season comes first. Sometimes it can be nice to display the bits in a ring, but usually bitloops are represented by bitstrings. Square brackets are replaced by parentheses to indicate the first and last bits are adjacent.
[100001] is a bitstring. (100001) is a bitloop.
Potentially multiple bitstrings may represent the same bitloop.
The bitstring [1000] represents the bitloop (1000). [0100], [0010] and [0001] may also represent the same bitloop.
The bitloop (1000) can also be written as (0100), (0010) or (0001).
I call a rotation class the set of all bitstrings that represent the same bitloop. The bitloop represents the rotation class as a whole. Bitstrings in a rotation class are rotations of each other.
(100) represents the rotation class {[100], [010], [001]}.
(1010) represents the rotation class {[1010], [0101]}. [1010] is a rotation of [0101] and vice versa.
The bitstring [11111] represents the bitloop (11111), which represents the rotation class {[11111]}.
A permutation of a bitstring alters the indices of its bits. Let α be a permutation that follows this rule:
α(i1) = i2, α(i2) = i3, ..., α(in-1) = in, α(in) = i1.
α is a cycle (or n-cycle), which rotates the indices by one position. αm rotates each index by m positions. α1 = α.
| α([1101]) = [1110] |
| α([1110]) = [0111] |
| α2([0111]) = [1101] |
| α-1([1101]) = [1011] |
Two bitstrings a and b are adjacent if α(a) = b or α(b) = a.
[0100] and [0010] are adjacent.
[1000] and [0010] are not adjacent.
The Link
A unary bitwise operation takes one bitstring and produces another. The unary operation bitwise NOT takes one bitstring and changes each zero to a one, and each one to a zero. The resulting bitstring is the inverse of the original, and vice versa.
| NOT | [0011] | |
| = | [1100] |
[0011] is the inverse of [1100], and [1100] is the inverse of [0011].
Bitloops can also be inverses of each other. If so, then members of their respective rotation classes form inverse pairs.
| Bitloop | Rotation class | ||
| (100) | [100] | [010] | [001] |
| (011) | [011] | [101] | [110] |
| ↑ | ↑ | ↑ | |
| inverse pairs | |||
A binary bitwise operation takes two bitstrings and produces another. Bitwise XOR does this by adding bits, where 0 + 0 = 0, 0 + 1 = 1, and 1 + 1 = 0. This kind of addition is called addition modulo 2.
| [0101] | ||
| XOR | [0011] | |
| = | [0110] |
I define a unary operation called the link. It takes one bitloop and produces another. “Link” also refers to the resulting bitloop. Given a bitloop P, take any pair of adjacent bitstrings from its rotation class and perform the bitwise XOR operation on them. Let the result belong to the rotation class represented by the bitloop Q. Then Q is the link of P.
Let P = (1000), a = [1000], b = [0100].
| [1000] | ||
| XOR | [0100] | |
| = | [1100] |
Then (1100) is the link of (1000).
I define sublink as the reverse operation, so P is the sublink of Q.
A bitloop and its link are written as an ordered pair.
((0011), (0101))
A series of links is written as a sequence.
((0001), (0011), (0101), (1111), (0000), (0000), ...)
A bitloop has a sublink if and only if it has an even number of ones.
The sublink of (11) is (01). (01) has no sublink.
A bitloop and its inverse generate the same link.
(11110) is the link of (01010) and (10101).
A bitloop that has an inverse is invertible. A bitloop that has no inverse is non-invertible. A bitloop is non-invertible if its rotation class consists of inverse pairs.
(1100) is non-invertible and represents {[1100], [1001], [0011], [0110]}.
A non-invertible bitloop can be split in half, so that the two halves are an inverse pair of bitstrings.
(1101100100) is non-invertible. [11011] and [00100] are inverses.
Some bitloops are their own link. The first six are listed below with their respective tessellations. Any reverses and repetitions of these are also their own link.
| n | tess. | bitloop |
| 1 | png | (0) |
| 3 | png | (011) |
| 7 | png | (0011101) |
| 15 | png | (000111101011001) |
| 21 | png | (000011111010100110001) |
| 63 | png | (000001000011000101001111010001110010010110111011001101010111111) |
Patterns
A bitloop has a pattern, which is another bitloop that iterates within it. A pattern must iterate a whole number of times, and match every bit in the bitloop with none left over. If there are multiple bitloops that satisfy this criteria, then the pattern is defined as the one with the fewest bits. Every bitloop has one and only one pattern.
(0001) is the pattern of (0001000100010001). (00010001) is not a pattern.
(1100) is not the pattern of (11001100110011), because it doesn’t iterate a whole number of times.
(000111011) is the pattern of (000111011).
Since a pattern is a bitloop, it may be represented by any bitstring in its rotation class. Some care should be taken so that a pattern is represented by a rotation that matches the greater bitloop’s rotation.
The pattern of (001001) is (001). [001] represents the pattern. [010] and [100] could also represent the pattern. While “(010) is a pattern of (001001)” is a true statement, it would be better to choose matching bitstrings to represent the respective bitloops. “(010) is a pattern of (010010)” has the same meaning, but is easier to comprehend.
Another way to display a bitloop is with the bits in a row and repeating indefinitely on either side. Here it becomes more apparent why a bitloop has only one pattern, and why that pattern is not a bitstring, but rather a bitloop.
... 0 1 1 0 1 1 1 1 0 1 1 0 1 1 1 1 0 1 1 0 1 1 1 1 0 1 1 0 1 1 1 1 0 1 1 0 1 1 1 ...
... 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 ...
... 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 ...
In such a display, the pattern must be guaranteed to iterate at least two times to identify it. A pattern is the pattern of arbitrarily many bitloops.
For ease of reference, a bitstring or bitloop may be represented by its pattern, if the value of n is implied, or the bitloop itself is not important. Parentheses may also be dropped.
(00001111, 0001, 0011, 01, 1, 0) is a series of links.
Power Sets
The notation P(S) is used to denote the power set of a set S. The power set is the set of all subsets of S. The calligraphic font is used for sets of sets.
Let S = {x, y} for the next four examples.
P(S) = {∅, {x}, {y}, {x, y}}, where ∅ denotes the empty set.
The elements of S can be assigned indices. Recall J, the set of indices. Define a function f: S → J, which assigns each element of S an index.
f(x) = i1, f(y) = i2
The bits of a bitstring are also indexed by J, so each element in S is assigned a position in a bitstring.
[ i1 i2 ] → [ x y ]
By this correspondence, a bitstring can represent an element of P(S). The value of each bit indicates whether or not the corresponding element of S is included in the element of P(S). P(n) is the set of all bitstrings having n bits. Every bitstring in P(n) represents an element of P(S).
| P(S) | P(2) |
| ∅ | [00] |
| {x} | [10] |
| {y} | [01] |
| {x, y} | [11] |
P(1) = {[0], [1]} is the first power set. “First” refers to having bitstrings with the fewest number of bits.
P(n) can be partitioned in a few ways. It can be partitioned by inverse pairs of bitstrings, because every bitstring has one and only one inverse, which is not itself. P(n) can be partitioned by rotation classes, because each bitstring belongs to one and only one rotation class. P(n) can also be partitioned according to the length of each bitstring’s pattern.
Let p denote the pattern of a bitstring x, and length(p) the number of bits in p. Another partition is {A, B, C}, where A, B and C are defined as follows: For every x in P(n), if length(p) = 1, then x ∈ A; if length(p) = n, then x ∈ C; otherwise, x ∈ B.
| P(4) = | {0000, 1111, 0101, 1010, 0011, 0110, 1100, 1001, 0001, 0010, 0100, 1000, 1110, 1101, 1011, 0111} |
| A = | {0000, 1111} |
| B = | {0101, 1010} |
| C = | {0011, 0110, 1100, 1001, 0001, 0010, 0100, 1000, 1110, 1101, 1011, 0111} |
For 0101, p = 01, and for 1010, p = 10. In either case, length(p) equals two. Two is greater than one and less than n, so 0101, 1010 ∈ B.
A = {0, 1} for any n, where bitstrings are represented by their respective patterns.
{A, B, C} can be utilized to prove a theorem about prime numbers:
Theorem. For any prime number n, 2n - 2 is divisible by n.
Proof. The set P(n) has 2n elements. Since n is prime and n must be divisible by the number of bits in p, length(p) = 1 or n, so B is empty. A has two elements, so C has 2n - 2 elements. Every bitstring in C belongs to a rotation class with n bitstrings, so the number of bitstrings in C is divisible by n. Therefore 2n - 2 is divisible by n. ∎
Let A = {a, b, c, d} be a subset of P(n), equipped with the operation bitwise XOR. Let a be the bitstring with all zeros and b be the bitstring with all ones. Let c and d be any other pair of inverse bitstrings. A is a Klein four-group, where a is the identity element.
Chains
A chain is a set of bitloops equipped with the link operation. For any bitloop in a chain, the link of that bitloop is also included, and so are its subinks, if they exist. A bitloop generates the chain it belongs to, because all of the chain’s bitloops can be derived by taking successive links and/or sublinks of that bitloop.

The link of 0 is 0, and the sublink of 0 is 1. 1 has no sublink, and its link is 0. 0 and 1 comprise the first chain.
For ease of reference, P(n) can be referred to as a set of bitloops, which are understood to represent rotation classes.
Yet another partition of P(n) is the gathering of bitloops into chains. Every bitstring belongs to a single bitloop, and every bitloop belongs to a single chain, so the partition of P(n) into bitloops is a refinement of the partition of P(n) into chains.
P(3) has eight bitstrings, which are partitioned into four rotation classes, which are partitioned into two chains.
All chains share a general structure. A chain includes one cycle, which is a subset of bitloops that form a loop of successive links. A cycle is written as a sequence. It’s implied that the first bitloop is the link of the last bitloop.
(00011, 10010, 11110) is the first cycle with multiple bitloops.
(000101, 111100) is the second cycle with multiple bitloops.
From every bitloop in the cycle there extends a tree of successive sublinks. A bitloop in a cycle is referred to as the root of its tree. The root has two sublinks: one in its tree, and one in the cycle. The tree ends with bitloops that have no sublinks, and these are referred to as leaves.
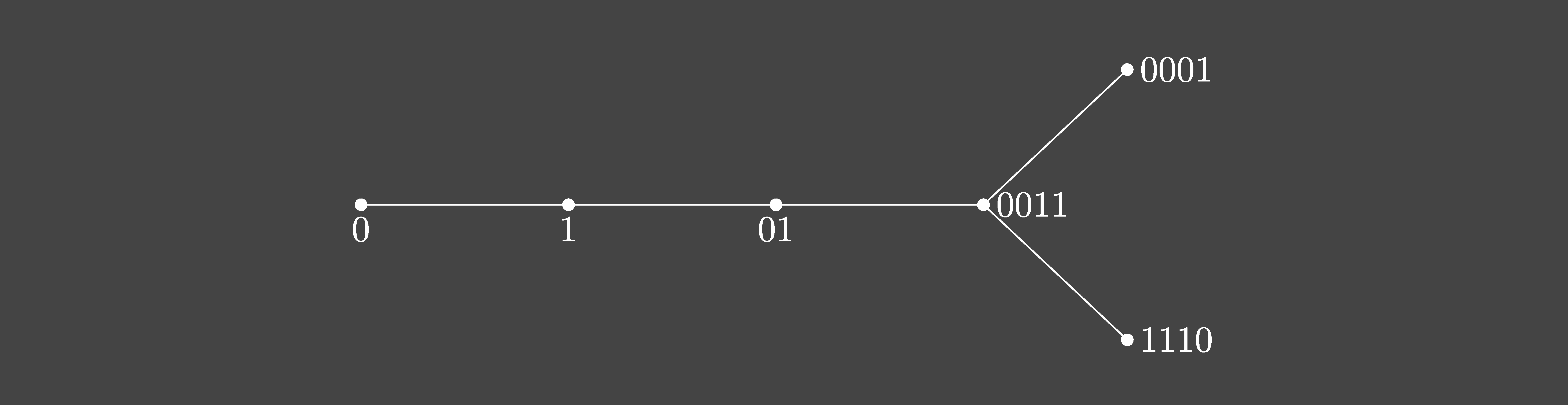
P(4) is partitioned by a single chain. The cycle of that chain has a single root, so the chain has only one tree. The sequence of successive sublinks beginning with the root is (0, 1, 01, 0011, 0001). 0011 also has the sublink 1110. 0001 and 1110 are the two leaves of the tree.
Trees vary in how many levels of successive sublinks they have.
The chain that comprises P(8) has nine levels of sublinks, including the root.
Restrict n to only powers of two. The chain that comprises P(n) has n + 1 levels of sublinks, including the root.
Trees also vary by what levels have invertible or non-invertible bitloops. The bitloops of a given level are either all invertible or all non-invertible. It follows that all of a tree’s direct paths from the root to a leaf have the same sequence of bitloop invertibility. This sequence I call the tree’s structure.
The structure can be written in the format (x0, x1, ..., xn-1) where n is the number of levels in the tree, and xi is how many sublinks the bitloop at level i has. The root is at level zero and has two sublinks, so the structure always begins with a two. The leaf of a tree has no sublinks, so the structure always ends with a zero.
| The structure of the one tree in ... | ||
| ... P(1) is (2, 0). | ||
| ... P(2) is (2, 1, 0). | ||
| ... P(4) is (2, 1, 1, 2, 0). | ||
| ... P(8) is (2, 1, 1, 2, 1, 2, 2, 2, 0). | ||
| ... P(16) is (2, 1, 1, 2, 1, 2, 2, 2, 1, 2, 2, 2, 2, 2, 2, 0, 0). | ||
For shorthand, the structure may be written as a string of digits.
The structure of the one tree in P(16) is 21121222122222200.
Symmetry
A bitstring is symmetric and non-reversible if the order of its bits is the same as the order in reverse. A bitstring that is not symmetric is asymmetric and reversible. Two asymmetric bitstrings form a reverse pair if they differ only by reversing the order of bits. Each is the reverse of the other.
[100010] and [010001] are asymmetric and form a reverse pair. [100001] is symmetric and non-reversible.
A bitloop is symmetric if its rotation class contains one symmetric bitstring. If the rotation class of a symmetric bitloop contains an asymmetric bitstring, then the reverse of the bitstring is also included.
(11010) is symmetric. Its rotation class includes one symmetric bitstring and two reverse pairs. {[11010], [01101], [10110], [01011], [10101]}
Every bitloop in P(5) is symmetric. {0, 1, 00001, 11110, 11100, 00011, 01101, 10010}
A bitloop is asymmetric if all the bitstrings in its rotation class are asymmetric. An asymmetric bitloop X has a reverse Y, such that the reverses of the bitstrings in the rotation class of X are contained in the rotation class of Y.
The rotation classes of (1001110) and (0111001) are displayed below with reverse pairs aligned vertically.
| {[1001110], [0011101], [0111010], [1110100], [1101001], [1010011], [0100111]} |
| {[0111001], [1011100], [0101110], [0010111], [1001011], [1100101], [1110010]} |
The bitloops of a given chain are either all symmetric or all asymmetric. Hence the symmetry of a chain is determined by the symmetry of its bitloops. Every asymmetric chain has a reverse: For any asymmetric chain X there exists an asymmetric chain Y which contains the reverses of all of the bitloops contained in X. A pair of asymmetric chains may be referred to as a single asymmetric chain.
(0001101) and (1110010) comprise the first asymmetric chain.
There is a geometric way to tell if a bitloop is symmetric or asymmetric. Arrange the bits in a ring, and see if a line of symmetry can be drawn. The line may pass through or between one or two bits.
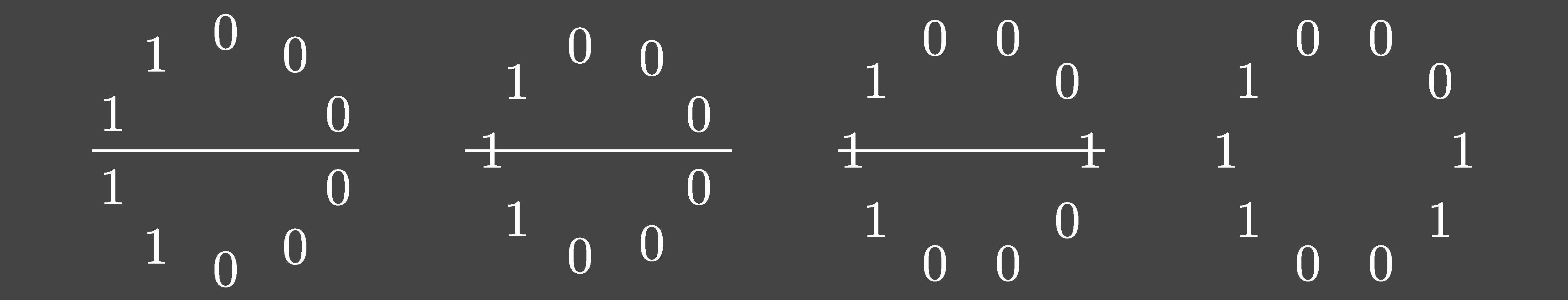
Graphs
A chain may be expressed as a graph, where bitloops are vertices and link operations are edges. A chain’s cycle is a subgraph. The order of a graph is the number of its vertices. Two chains are isomorphic if they share the same graph, or equivalently, they have the same cycle order and structure.

Three chains in P(11) are isomorphic. Their graph has cycle order 31 and structure (2, 0).
Let x < y. The graph of the chain that comprises P(2x) is a subgraph of the graph of the chain that comprises P(2y)
P(21) has 2,097,152 bitstrings. They are partitioned into 99,880 rotation classes, which are partitioned into 418 chains (398 of which are asymmetric pairs), which are partitioned into 6 graphs. All six graphs have the structure (2, 0). Their cycle orders are 1, 3, 7, 9, 21 and 63.
Isometric chains may or may not share the same symmetry.
The chain generated by (000000001) is symmetric, and the chain generated by (000001011) is asymmetric. Both chains have cycle order 7 and structure (2, 0).

The chain generated by (0000000001) is symmetric, and the chain generated by (0000001011) is asymmetric. Both chains have cycle order 6 and structure (2, 2, 0).
Isometric chains may or may not have the same number of bitstrings. This is because their respective patterns aren’t necessarily the same length.
P(12) contains two isometric chains with six bitloops each. Each chain has a single bitloop at its core. One chain has 16 bitstrings, and the other has 48. Their respective cores are (0) and (011).
Tessellations
From any cycle may be derived a tessellation. First the bitloops in the cycle are displayed so that each bitloop is above its sublink and below its link. The top bitloop is the sublink of the bottom bitloop. Bitloops are vertically aligned to show the sum modulo 2 of two bits is above and between them.
| 0 | 1 | 0 | 0 | 1 | |||||
| 1 | 0 | 0 | 0 | 1 | |||||
| 0 | 1 | 1 | 1 | 1 |
Successive links can continue upwards, and they’ll still be part of the same cycle. Likewise, each bitloop can iterate horizontally, as if it were the pattern of one longer bitloop. The link operation will work as expected. Denote A1/n as the pattern of A, such that A1/n iterates n times within A. Let a bitloop B1/n be the link of A1/n. Then B is the link of A.
| 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | ||||||||||
| 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | ||||||||||
| 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | ||||||||||
| 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | ||||||||||
| 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | ||||||||||
| 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 |
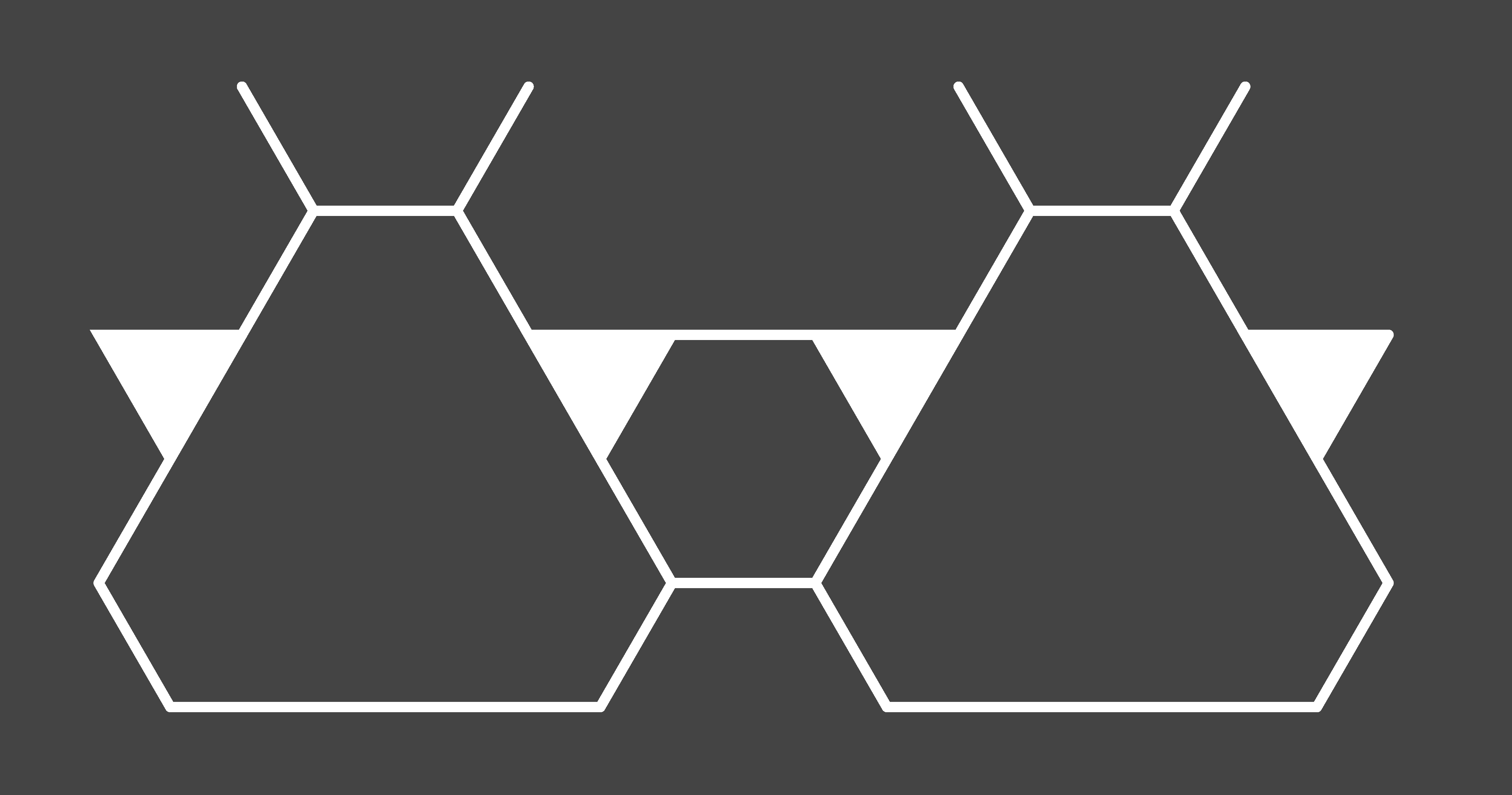
In this way a cycle is a unit of tessellation. Iterations can be displayed for visual, rather than numeric interpretation. One method is used in the tessellations that follow. Zeros and ones are replaced with lines and triangles. Lines connect the positions of ones, and any inverted triangles are filled.
See how the figure below matches the zeros and ones above.
Catalogue
The following .pdf files show the complete graphs and chains of the power sets up to n = 14. The pattern of every bitloop of every chain is listed. Graphs are named Gx-y, where x is the graph’s cycle order, and y is the graph’s structure. The same graph can appear in multiple power sets.
P(1) has one graph, called G1-20. It appears in every power set where n is odd.
G1-21120 appears in P(4), P(12) and P(20).
P(5) is the first power set with two graphs. They are named G1-20 and G3-20.
Chains are named Cn-x-i, where n is the first power set that the chain belongs to, x is again the chain’s cycle order, and i is an index of chains that belong to the same graph. The name is appended with an “a” if the chain is asymmetric. This implies the chain’s reverse pair. Some chains appear in multiple power sets, because their patterns are the same.
C7-1-1a is the first asymmetric chain.
C1-1-1 appears in all power sets where n is odd.
The following .csv files describe power sets up to n = 28, including details about each graph and chain, such as its size and structure.
The following .pdf files show all tessellations up to n = 14. Tessellations are named Tn-x-y, where Cn-x-y is the first chain from which Tn-x-y is derived.
Appendix
From this question on StackExchange.
Bitstrings can be considered as vectors in a vector space. Then the rotation, link, and sublink operations can be considered linear transformations that are represented by matrices. Their corresponding matrices are as follows, where n is the number of rows and columns:
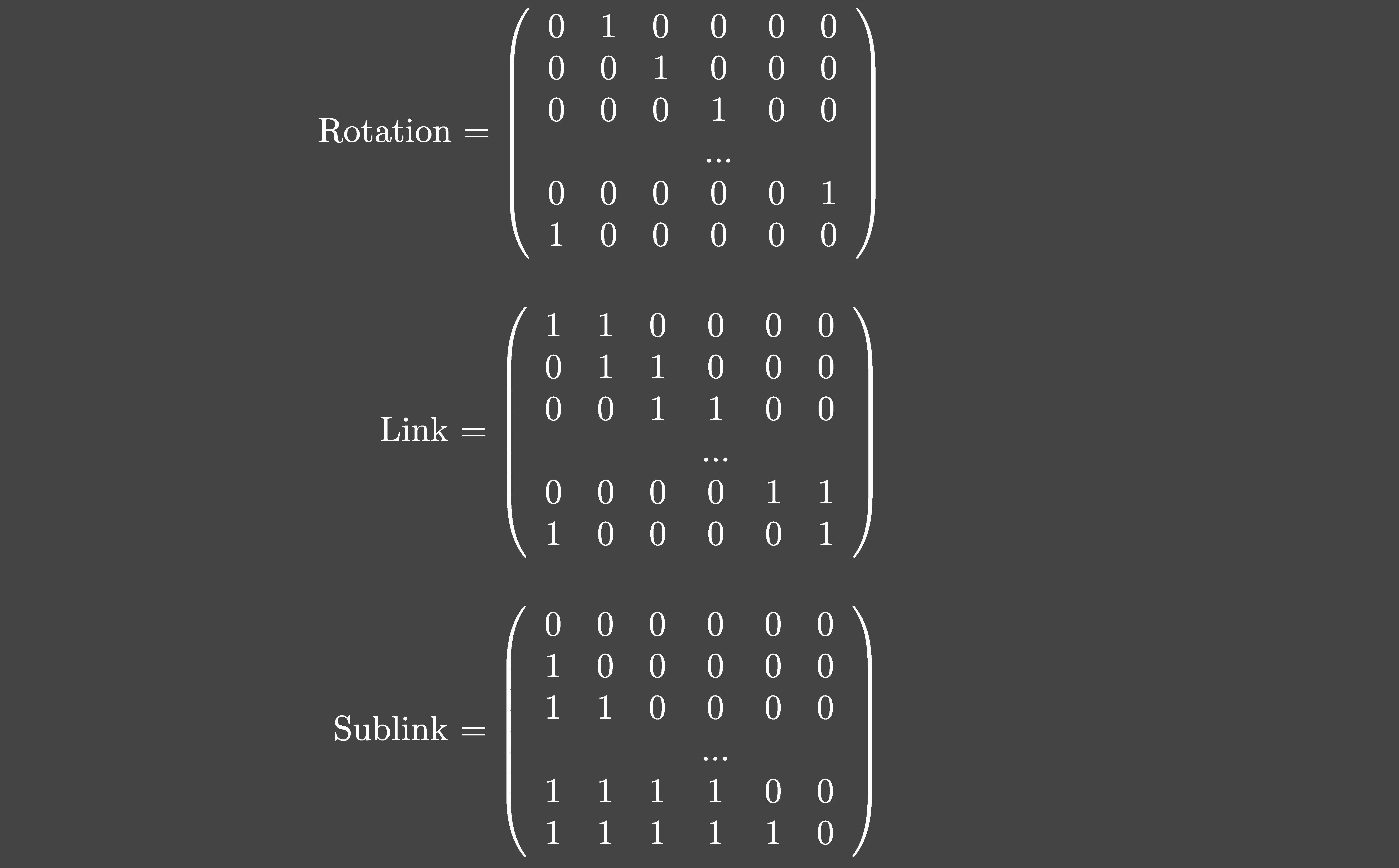
The link matrix is the sum of the rotation matrix with the identity matrix.
The input and output of each operation is a bitstring, so for the link and sublink operations, these bitstrings represent bitloops. While a bitloop with an odd number of ones has no sublink, the sublink matrix will still produce an output that doesn’t represent a true sublink. Also, while a bitloop may have two sublinks, the sublink matrix will only produce one output. The output and its inverse represent the two sublinks.